查看数据源：6256388cea59ab000a73e4bd
在 $Rt\bigtriangleup ABC$ 中，$\angle C=90^\circ , BC=3, AC=6, D, E$ 分别是 $AC, AB$ 上的点，满足 $DE\parallel BC$ 且 $DE$ 经过 $\bigtriangleup ABC$ 的重心，将 $\bigtriangleup ADE$ 沿 $DE$ 折起到 $\bigtriangleup A_1DE$ 的位置，使 $A_1C\perp CD, M$ 是 $A_1D$ 的中点，如图所示．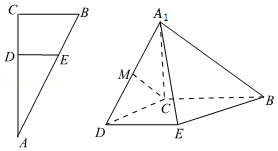
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    线面垂直
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的角
    >
    线面角
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的垂直关系
    >
    面面垂直
  1. 求证：$A_1C\perp$ 平面 $BCDE$；
    标注
    • 知识点
      >
      立体几何
      >
      空间位置关系
      >
      空间的垂直关系
      >
      线面垂直
    答案
    略
    解析
    略
  2. 求 $CM$ 与平面 $A_1BE$ 所成角的大小；
    标注
    • 知识点
      >
      立体几何
      >
      空间几何量
      >
      空间的角
      >
      线面角
    答案
    （2）$ \dfrac{\pi}{4}$
    解析
    略
  3. 在线段 $A_1B$ 上是否存在点 $N(N$ 不与端点 $A_1, B$ 重合），使平面 $CMN$ 与平面 $DEN$ 垂直？若存在，求出 $A_1N$ 与 $BN$ 的比值；若不存在，请说明理由．
    标注
    • 知识点
      >
      立体几何
      >
      空间位置关系
      >
      空间的垂直关系
      >
      面面垂直
    答案
    （3）$ \dfrac{A_1N}{BN}=2$
    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2 问题3 答案3 解析3 备注3
0.109143s