固定抛物线上一点 $A\left(\dfrac {a^2}{4},a\right)(a>0)$，考虑对于不同的 $a$，满足 $\angle FAM$ 为锐角时 $m$ 的取值集合，再求交集．于是考虑边界情况 $\angle FAM=90^\circ$ 时 $M$ 的位置，如下图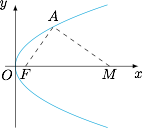：对 $a$ 进行讨论，当 $a=2$ 时，$\angle FAM$ 恒为锐角；
当 $a\ne 2$ 时，过点 $A$，且垂直于 $FA$ 的直线方程为$$y-a=-\dfrac {\frac{a^2}{4}-1}{a}\left(x-\dfrac {a^2}{4}\right ),$$令 $y=0$ 得直线 $MA$ 的横截距$$ x_a=\dfrac {4a^2}{a^2-4}+\dfrac {a^2}{4}=5+\dfrac{16}{a^2-4}+\dfrac{a^2-4}{4},$$当 $a<2$ 时，$a^2-4\in (-4,0)$，此时 $x_a<0$，结合图象知，此时对任意的 $m>0$，都有 $\angle FAM$ 为锐角；
当 $a>2$ 时，$x_a\geqslant 9$，当且仅当 $a^2=12$ 时取等号．结合图象知，对任意的 $a>2$，$m$ 在集合 $\left(0,x_a\right)$ 内，且 $m\ne 1$，故满足条件的 $m$ 的集合为 $(0,1)\cup(1,9)$．
综上知 $m\in(0,1)\cup(1,9)$．