已知函数 $f\left(x\right)=\begin{cases}
x^3,&x\leqslant a,\\
x^2,&x>a,
\end{cases}$ 若存在实数 $b$，使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点，则 $a$ 的取值范围是 ．
x^3,&x\leqslant a,\\
x^2,&x>a,
\end{cases}$ 若存在实数 $b$，使函数 $g\left(x\right)=f\left(x\right)-b$ 有两个零点，则 $a$ 的取值范围是
【难度】
【出处】
2015年高考湖南卷（理）
【标注】
【答案】
$(-\infty ,0)\cup (1,+\infty )$
【解析】
函数 $y=x^3$ 与 $y=x^2$ 的公共点为 $(0,0)$ 和 $(1,1)$，因此按 $a$ 与分界点 $0$ 和 $1$ 的相对大小展开讨论：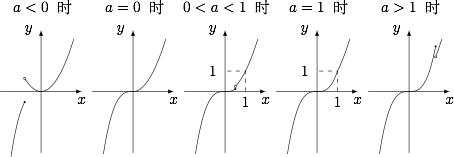
由图不难得到 $a$ 的取值范围是 $a<0$ 或 $a>1$．
由图不难得到 $a$ 的取值范围是 $a<0$ 或 $a>1$．
题目
答案
解析
备注
