已知 $\omega>0$，在函数 $y=2\sin {\omega x}$ 与 $y=2\cos {\omega x}$ 的图象的交点中，距离最短的两个交点的距离为 $2\sqrt 3$，则 $\omega$ = ．
【难度】
【出处】
2015年高考湖南卷（文）
【标注】
【答案】
$\dfrac{\pi}{2}$
【解析】
注意到函数的周期性和对称性，只需要考虑两个函数在区间 $\left[0,\dfrac{2\pi}{\omega}\right]$ 内的函数图象，如图．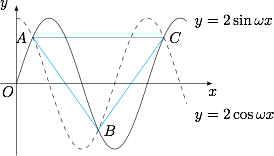
由于交点的横坐标即方程 $2\sin\omega x=2\cos\omega x$ 的解，可得 $\omega x=k\pi+\dfrac{\pi}4$（$k\in{\mathbb Z}$），因此交点的纵坐标必然为 $\pm \sqrt 2$．如图，设相邻的三个交点为 $A(x_1,\sqrt 2)$，$B(x_2,-\sqrt 2)$，$C(x_3,\sqrt 2)$，则根据题意有$$\min\{|AB|,|AC|\}=2\sqrt 3,$$若 $|AB|=2\sqrt 3$，可得$$\left(\dfrac{\pi}{\omega}\right)^2+(2\sqrt 2)^2=(2\sqrt 3)^2,$$解得 $\omega=\dfrac{\pi}2$，此时 $|AC|=\dfrac{2\pi}{\omega}=4>2\sqrt 3$，符合题意．
若 $|AC|=2\sqrt 3$，可得 $\dfrac{2\pi}{\omega}=2\sqrt 3$，此时$$|AB|=\sqrt{\left(\dfrac{\pi}{\omega}\right)^2+(2\sqrt 2)^2}=\sqrt{11}<2\sqrt 3,$$不符合题意．
因此 $\omega$ 的值为 $\dfrac{\pi}{2}$．
由于交点的横坐标即方程 $2\sin\omega x=2\cos\omega x$ 的解，可得 $\omega x=k\pi+\dfrac{\pi}4$（$k\in{\mathbb Z}$），因此交点的纵坐标必然为 $\pm \sqrt 2$．如图，设相邻的三个交点为 $A(x_1,\sqrt 2)$，$B(x_2,-\sqrt 2)$，$C(x_3,\sqrt 2)$，则根据题意有$$\min\{|AB|,|AC|\}=2\sqrt 3,$$若 $|AB|=2\sqrt 3$，可得$$\left(\dfrac{\pi}{\omega}\right)^2+(2\sqrt 2)^2=(2\sqrt 3)^2,$$解得 $\omega=\dfrac{\pi}2$，此时 $|AC|=\dfrac{2\pi}{\omega}=4>2\sqrt 3$，符合题意．若 $|AC|=2\sqrt 3$，可得 $\dfrac{2\pi}{\omega}=2\sqrt 3$，此时$$|AB|=\sqrt{\left(\dfrac{\pi}{\omega}\right)^2+(2\sqrt 2)^2}=\sqrt{11}<2\sqrt 3,$$不符合题意．
因此 $\omega$ 的值为 $\dfrac{\pi}{2}$．
题目
答案
解析
备注
