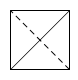
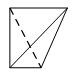
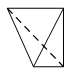
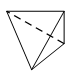
一个四面体的顶点在空间直角坐标系 $O - xyz$ 中的坐标分别是 $\left( {1,0,1} \right)$，$\left( {1,1,0} \right)$，$\left( {0,1,1} \right)$，$\left( {0,0,0} \right)$，画该四面体三视图中的正视图时，以 $zOx$ 平面为投影面，则得到正视图可以为 \((\qquad)\)
A:
B:
C:
D:
【难度】
【出处】
2013年高考新课标Ⅱ卷（理）
【标注】
【答案】
A
【解析】
本题考查平行投影及三视图的画法．将四面体在空间直角坐标系中画出，再得出正视图即可．根据各顶点的坐标作出四面体的直观图如图所示：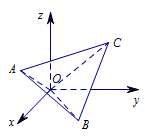
过点 $B$，$C$ 作 面 $zOx$ 的垂线，如图：
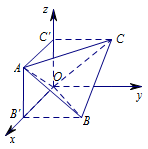则该四面体以 $zOx$ 平面为投影面的正视图为：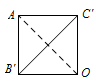
过点 $B$，$C$ 作 面 $zOx$ 的垂线，如图： 则该四面体以 $zOx$ 平面为投影面的正视图为：
题目
答案
解析
备注
