若圆内接四边形 $ABCD$ 的边长 $AB = 4$，$BC = 8$，$CD = 9$，$DA = 7$，则 $\cos A = $ ．
【难度】
【出处】
2002年上海交通大学保送生连读班考试
【标注】
【答案】
$ - \dfrac{2}{5}$
【解析】
如图，连接 $BD$．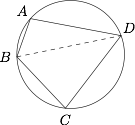
在 $\triangle ABD$ 中，$$B{D^2} = A{B^2} + A{D^2} - 2\cos A \cdot AB \cdot AD = 65 - 56\cos A,$$在 $\triangle BCD$ 中，$$B{D^2} = B{C^2} + C{D^2} - 2\cos C \cdot BC \cdot CD = 145 + 144\cos A.$$于是 $\cos A = - \dfrac{2}{5}$．
在 $\triangle ABD$ 中，$$B{D^2} = A{B^2} + A{D^2} - 2\cos A \cdot AB \cdot AD = 65 - 56\cos A,$$在 $\triangle BCD$ 中，$$B{D^2} = B{C^2} + C{D^2} - 2\cos C \cdot BC \cdot CD = 145 + 144\cos A.$$于是 $\cos A = - \dfrac{2}{5}$．
题目
答案
解析
备注
