某市环形马路上顺次有 $A,B,C,D,E$ 五所小学,各小学分别有电脑 $15,7,11,3,14$ 台,现在为使各小学的电脑数相等,各向相邻小学移交若干台,且要使移交的电脑的总台数最小,因此,从 $A$ 向 $B$ 移交了 台,从 $B$ 向 $C$ 移交了 台,从 $A$ 向 $E$ 移交了 台,移动总数是 台.
【难度】
【出处】
2002年上海交通大学保送生连读班考试
【标注】
【答案】
$3$;$0$;$2$;$12$
【解析】
最终每个小学的电脑总数为 $10$ 台.于是 $A,B,C,D,E$ 五所小学分别需要转移 $ - 5,3, - 1,7, - 4$ 台电脑.(其中负号表示向外转移).
由于 $A$ 与 $D$ 不相邻,于是至少需要移动 $12$ 台电脑.
如图所示,为移动总数为 $12$ 台的方案.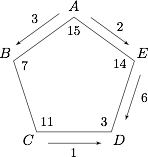
由于 $A$ 与 $D$ 不相邻,于是至少需要移动 $12$ 台电脑.
如图所示,为移动总数为 $12$ 台的方案.

题目
答案
解析
备注