已知函数 $f\left( x \right) = {x^3} + a{x^2} + bx + c$，下列结论中错误的是 \((\qquad)\)
【难度】
【出处】
2013年高考新课标Ⅱ卷（理）
【标注】
【答案】
C
【解析】
本题考查三次函数的图象与性质，借助导数工具进行研究．因为函数 $ f\left(x\right) $ 的值域为 $ {\mathbb{R}} $，所以一定存在 $ {x_0} \in {\mathbb{R}}$，使得 $f\left( {x_0} \right) = 0$，A正确；
假设函数 $f\left( x \right) = {x^3} + a{x^2} + bx + c$ 的对称中心为 $ \left(m,n\right) $，将函数的图象向左平移 $ m $，再向下平移 $ n $，则所得函数 $ y=f\left(x+m\right)-n $是奇函数，所以\[ f\left(x+m\right)+f\left(-x+m\right)-2n=0,\]化简得\[ \left(3m+a\right)x^2+m^3+am^2+bm+c-n=0. \]上式对 $ x\in \mathbb R $ 成立，故 $3m+a=0 $，得 $ m=-\dfrac a3 $，$ n=m^3+am^2+bm+c=f\left(-\dfrac a3\right)$，所以函数 $ f\left(x\right) $ 的对称中心为 $ \left(-\dfrac a3,f\left(-\dfrac a3\right)\right) $，故函数 $y = f\left( x \right)$ 的图象是中心对称图形，B正确；
由于 $f'\left(x\right)=3x^2+2ax+b $ 是开口向上的二次函数，若 ${x_0}$ 是 $f\left( x \right)$ 的极小值点，如图：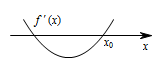
则 $f\left( x \right)$ 在区间 $\left( { - \infty ,{x_0}} \right)$ 不单调，C错误；
若 ${x_0}$ 是 $f\left( x \right)$ 的极值点，则一定有 $f'\left( {x_0} \right) = 0$，D正确．
假设函数 $f\left( x \right) = {x^3} + a{x^2} + bx + c$ 的对称中心为 $ \left(m,n\right) $，将函数的图象向左平移 $ m $，再向下平移 $ n $，则所得函数 $ y=f\left(x+m\right)-n $是奇函数，所以\[ f\left(x+m\right)+f\left(-x+m\right)-2n=0,\]化简得\[ \left(3m+a\right)x^2+m^3+am^2+bm+c-n=0. \]上式对 $ x\in \mathbb R $ 成立，故 $3m+a=0 $，得 $ m=-\dfrac a3 $，$ n=m^3+am^2+bm+c=f\left(-\dfrac a3\right)$，所以函数 $ f\left(x\right) $ 的对称中心为 $ \left(-\dfrac a3,f\left(-\dfrac a3\right)\right) $，故函数 $y = f\left( x \right)$ 的图象是中心对称图形，B正确；
由于 $f'\left(x\right)=3x^2+2ax+b $ 是开口向上的二次函数，若 ${x_0}$ 是 $f\left( x \right)$ 的极小值点，如图：
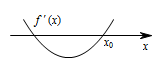则 $f\left( x \right)$ 在区间 $\left( { - \infty ,{x_0}} \right)$ 不单调，C错误；若 ${x_0}$ 是 $f\left( x \right)$ 的极值点，则一定有 $f'\left( {x_0} \right) = 0$，D正确．
题目
答案
解析
备注
