在等腰梯形 $ABCD$ 中，已知 $AB \parallel DC$，$AB=2$，$BC=1$，$\angle ABC =60^\circ$．动点 $E$ 和 $F$ 分别在线段 $BC$ 和 $DC$ 上，且 $\overrightarrow {BE}=\lambda \overrightarrow {BC}$，$\overrightarrow {DF}=\dfrac {1}{9\lambda }\overrightarrow {DC}$，则 $\overrightarrow {AE}\cdot \overrightarrow {AF}$ 的最小值为 ．
【难度】
【出处】
2015年高考天津卷（理）
【标注】
【答案】
$\dfrac{29}{18}$
【解析】
如图，以 $A$ 为原点建立平面直角坐标系，$B(2,0)$，$C\left(\dfrac 32,\dfrac{\sqrt 3}2\right)$，$D\left(\dfrac 12,\dfrac{\sqrt 3}2\right)$．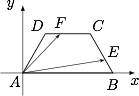
于是\[\begin{split} \overrightarrow {AE}\cdot \overrightarrow {AF}&=\left((1-\lambda)\overrightarrow {AB}+\lambda\overrightarrow {AC}\right)\cdot\left(\left(1-\dfrac{1}{9\lambda}\right)\overrightarrow {AD}+\dfrac{1}{9\lambda}\overrightarrow {AC}\right)\\
&=\dfrac{17}{18}+\dfrac {\lambda}2+\dfrac{2}{9\lambda}\\
&\geqslant \dfrac{17}{18}+2\sqrt {\dfrac{\lambda}2\cdot\dfrac{2}{9\lambda}}=\dfrac{29}{18},\end{split}\]其中等号当且仅当 $\lambda=\dfrac 23$ 时取得．
于是\[\begin{split} \overrightarrow {AE}\cdot \overrightarrow {AF}&=\left((1-\lambda)\overrightarrow {AB}+\lambda\overrightarrow {AC}\right)\cdot\left(\left(1-\dfrac{1}{9\lambda}\right)\overrightarrow {AD}+\dfrac{1}{9\lambda}\overrightarrow {AC}\right)\\&=\dfrac{17}{18}+\dfrac {\lambda}2+\dfrac{2}{9\lambda}\\
&\geqslant \dfrac{17}{18}+2\sqrt {\dfrac{\lambda}2\cdot\dfrac{2}{9\lambda}}=\dfrac{29}{18},\end{split}\]其中等号当且仅当 $\lambda=\dfrac 23$ 时取得．
题目
答案
解析
备注
