若 ${\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1$，则 $\dfrac{{y - 1}}{{x - 3}}$ 的取值范围是 ．
【难度】
【出处】
2003年复旦大学保送生招生测试
【标注】
【答案】
$\left[ { - \dfrac{{\sqrt 3 }}{3} , \dfrac{{\sqrt 3 }}{3}} \right]$
【解析】
问题即求圆 ${\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1$ 上的点与点 $A(3,1)$ 的连线的斜率范围，如图．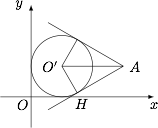
圆心为 $O'\left( {1,1} \right)$，过 $A$ 作圆的两条切线，其中一个切点为 $H$，设 $AH$ 的倾角为 $\theta $，则 $\tan \theta = \tan \angle O'AH = \dfrac{{\sqrt 3 }}{3}$，同样的可得另外一条切线的斜率为 $ - \dfrac{{\sqrt 3 }}{3}$．于是所求的范围为 $\left[ { - \dfrac{{\sqrt 3 }}{3},\dfrac{{\sqrt 3 }}{3}} \right]$．
圆心为 $O'\left( {1,1} \right)$，过 $A$ 作圆的两条切线，其中一个切点为 $H$，设 $AH$ 的倾角为 $\theta $，则 $\tan \theta = \tan \angle O'AH = \dfrac{{\sqrt 3 }}{3}$，同样的可得另外一条切线的斜率为 $ - \dfrac{{\sqrt 3 }}{3}$．于是所求的范围为 $\left[ { - \dfrac{{\sqrt 3 }}{3},\dfrac{{\sqrt 3 }}{3}} \right]$．
题目
答案
解析
备注
