边长为 $4$ 的正方形 $ABCD$ 沿 $BD$ 折成 $60^\circ $ 的二面角，则 $BC$ 中点与 $A$ 的距离是 ．
【难度】
【出处】
2003年复旦大学保送生招生测试
【标注】
【答案】
$2\sqrt 2 $
【解析】
如图．设 $BD$ 的中点为 $O$，则二面角的平面角 $\angle AOC = 60^\circ $，且 $AO = OC = AC 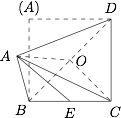= 2\sqrt 2 $．
在 $\triangle ABC$ 中，设 $BC$ 中点为 $E$，由中线长公式，可得 $AE = 2\sqrt 2 $．
在 $\triangle ABC$ 中，设 $BC$ 中点为 $E$，由中线长公式，可得 $AE = 2\sqrt 2 $．
题目
答案
解析
备注
