用长度为 $12$ 的篱笆围成四边形，一边靠墙，则所围成面积 $S$ 的最大值是 ．
【难度】
【出处】
2003年上海交通大学冬令营选拔测试
【标注】
【答案】
$12\sqrt 3 $
【解析】
如图．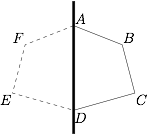
将 $ABCD$ 沿墙面作对称．
则六边形 $ABCDEF$ 的周长为 $24$，其最大面积为$$6 \cdot \dfrac{{\sqrt 3 }}{4} \cdot {\left( {\dfrac{{24}}{6}} \right)^2} = 24\sqrt 3 .$$所以所围成面积 $S$ 的最大值为 $12\sqrt 3 $．
将 $ABCD$ 沿墙面作对称．则六边形 $ABCDEF$ 的周长为 $24$，其最大面积为$$6 \cdot \dfrac{{\sqrt 3 }}{4} \cdot {\left( {\dfrac{{24}}{6}} \right)^2} = 24\sqrt 3 .$$所以所围成面积 $S$ 的最大值为 $12\sqrt 3 $．
题目
答案
解析
备注
