设 $a > 0$ 且 $a \ne 1$,则方程 ${a^x} + 1 = - {x^2} + 2x + 2a$ 的解的个数为 .
【难度】
【出处】
2007年上海交通大学冬令营选拔测试
【标注】
【答案】
$2$
【解析】
原方程等价于$${a^x}-2a = - {\left( {x - 1} \right)^2}.$$设 $f(x)=a^x-2a$,$g(x)=-(x-1)^2$,则抛物线 $g(x)$ 的顶点在函数 $f(x)$ 的图象上方,且开口向下,考虑到函数 $f(x)$ 下凸,$g(x)$ 上凸,于是原方程的解的个数为 $2$.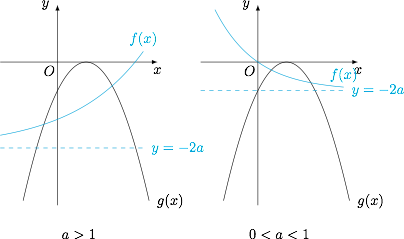

题目
答案
解析
备注