设关于 $x,y$ 的不等式 $x\left( {x - 1} \right) \leqslant y\left( {1 - y} \right)$ 与 ${x^2} + {y^2} \leqslant k$ 的解集分别为 $M$ 和 $N$．若 $M \subseteq N$，则 $k$ 的最小值为 ．
【难度】
【出处】
2007年上海交通大学冬令营选拔测试
【标注】
【答案】
$2$
【解析】
由$$x\left( {x - 1} \right) \leqslant y\left( {1 - y} \right) ,$$得$${x^2} + {y^2} - x - y \leqslant 0 ,$$即$$ {\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y - \dfrac{1}{2}} \right)^2} \leqslant \dfrac{1}{2}.$$如图，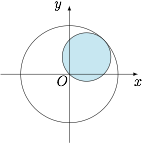
$k \geqslant 2$．
$k \geqslant 2$．
题目
答案
解析
备注
