查看数据源：599165c22bfec200011e0537
如图，有一个水平放置的透明无盖的正方体容器，容器高 $8 \mathrm{cm}$，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为 $6 \mathrm{cm}$，如果不计容器的厚度，则球的体积为 \((\qquad)\)  
A: $\dfrac{{500{\mathrm \pi} }}{3} \mathrm{cm}^3$
B: $\dfrac{{866{\mathrm \pi} }}{3} \mathrm{cm}^3$
C: $\dfrac{{1372{\mathrm \pi} }}{3} \mathrm{cm}^3$
D: $\dfrac{{2048{\mathrm \pi} }}{3} \mathrm{cm}^3$
【难度】
【出处】
2013年高考新课标I卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    旋转体
    >
    球
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
【答案】
A
【解析】
本题考查球的性质，分析条件计算球的半径即可．设正方体上底面截球所得小圆的圆心为 $M$，则 $M$ 为正方体上底面的中心，如图所示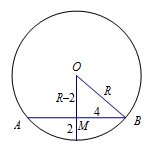： 设球的半径为 $R$，则\[R^2=\left(R-2\right)^2+4^2,\]解得 $R=5$，所以球的体积为 $\dfrac{{500{\mathrm \pi} }}{3} \mathrm{cm}^3$．
题目 答案 解析 备注
0.110770s