某几何体的三视图如图所示，则该几何的体积为 \((\qquad)\) 
【难度】
【出处】
2013年高考新课标I卷（理）
【标注】
【答案】
A
【解析】
本题考查组合体三视图还原的知识．根据主视图中的半圆，推测几何体可能由半圆柱构成为关键．由三视图知该几何体是由上部的长方体和下部的半圆柱构成的组合体（如图）．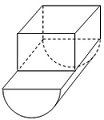
所以其体积\[\begin{split}V&\overset{\left[a\right]}=4\cdot2\cdot2+\dfrac12{\mathrm \pi} \cdot2^2\cdot4\\&=16 + 8{\mathrm \pi} .\end{split}\]（推导中用到[a]）
所以其体积\[\begin{split}V&\overset{\left[a\right]}=4\cdot2\cdot2+\dfrac12{\mathrm \pi} \cdot2^2\cdot4\\&=16 + 8{\mathrm \pi} .\end{split}\]（推导中用到[a]）
题目
答案
解析
备注
