如图，已知平面四边形 $ABCD$，$AB=BC=3$，$CD=1$，$AD=\sqrt 5$，$\angle ADC=90^\circ $．沿直线 $AC$ 将 $\triangle ACD$ 翻折成 $\triangle ACD'$，直线 $AC$ 与 $BD'$ 所成角的余弦的最大值是 ．
【难度】
【出处】
2016年高考浙江卷（文）
【标注】
【答案】
$\dfrac{\sqrt 6}6$
【解析】
过 $D$ 作 $DH$ 垂直 $AC$ 于 $H$，如图，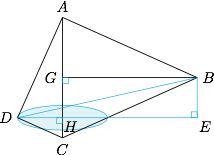
点 $D'$ 在以 $H$ 为圆心，$DH$ 为半径的圆上运动，且圆面（记为 $\alpha$）与 $AC$ 垂直．
在 $D$ 点运动的过程中，直线 $AC$ 与 $BD'$ 所成角为直线 $BD'$ 与圆面 $\alpha$ 所成角的余角，因此问题等价于求直线 $BD'$ 与圆面 $\alpha$ 所成角的正弦值的最大值．
设 $E$ 为 $B$ 在圆面 $\alpha$ 上的投影，经计算得$$AC=\sqrt 6,$$进而$$D'H=DH=\dfrac{\sqrt {30}}6,EH=\dfrac{\sqrt{30}}2,EB=\dfrac{\sqrt 6}3,$$因此直线 $BD'$ 与圆面 $\alpha$ 所成角的正切值的最大值为$$\dfrac{EB}{EH-D'H}=\dfrac{1}{\sqrt 5},$$于是其正弦值的最大值是 $\dfrac{\sqrt{6}}6$，即直线 $AC$ 与 $BD'$ 所成角的余弦的最大值为 $\dfrac{\sqrt{6}}6$．
点 $D'$ 在以 $H$ 为圆心，$DH$ 为半径的圆上运动，且圆面（记为 $\alpha$）与 $AC$ 垂直．在 $D$ 点运动的过程中，直线 $AC$ 与 $BD'$ 所成角为直线 $BD'$ 与圆面 $\alpha$ 所成角的余角，因此问题等价于求直线 $BD'$ 与圆面 $\alpha$ 所成角的正弦值的最大值．
设 $E$ 为 $B$ 在圆面 $\alpha$ 上的投影，经计算得$$AC=\sqrt 6,$$进而$$D'H=DH=\dfrac{\sqrt {30}}6,EH=\dfrac{\sqrt{30}}2,EB=\dfrac{\sqrt 6}3,$$因此直线 $BD'$ 与圆面 $\alpha$ 所成角的正切值的最大值为$$\dfrac{EB}{EH-D'H}=\dfrac{1}{\sqrt 5},$$于是其正弦值的最大值是 $\dfrac{\sqrt{6}}6$，即直线 $AC$ 与 $BD'$ 所成角的余弦的最大值为 $\dfrac{\sqrt{6}}6$．
题目
答案
解析
备注
