已知函数 $f\left(x\right) = {\begin{cases}
- {x^2} + 2x,x \leqslant 0, \\
\ln \left(x + 1\right),x > 0, \\
\end{cases}}$ 若 $|f\left(x\right)| \geqslant ax$，则 $a$ 的取值范围是 \((\qquad)\)
- {x^2} + 2x,x \leqslant 0, \\
\ln \left(x + 1\right),x > 0, \\
\end{cases}}$ 若 $|f\left(x\right)| \geqslant ax$，则 $a$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2013年高考新课标I卷（理）
【标注】
【答案】
D
【解析】
做出函数 $\lvert f \left( x\right)\rvert$ 的图象，寻找临界状态．作出函数 $y = \left|f\left(x\right) \right|$ 的图象如图：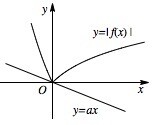
当 $ \left|f\left(x\right) \right| \geqslant ax$ 时，必有 $k \leqslant a \leqslant 0$，其中 $k$ 是 $y = {x^2} - 2x \left(x \leqslant 0 \right)$ 在原点处的切线斜率，显然，$k = - 2$．所以 $a$ 的取值范围是 $ \left[ - 2,0 \right]$．
当 $ \left|f\left(x\right) \right| \geqslant ax$ 时，必有 $k \leqslant a \leqslant 0$，其中 $k$ 是 $y = {x^2} - 2x \left(x \leqslant 0 \right)$ 在原点处的切线斜率，显然，$k = - 2$．所以 $a$ 的取值范围是 $ \left[ - 2,0 \right]$．
题目
答案
解析
备注
