将 $3$ 个 $12{\rm {cm}}×12{\rm cm}$ 的正方形沿邻边的中点剪开,分成两部分,如图,将这 $6$ 部分接于一个边长为 $6\sqrt 2 $ 的正六边形上(如下图),若拼接后的图形是一个多面体的表面展开图,该多面体的体积为 .

【难度】
【出处】
2005年上海交通大学保送推优生考试
【标注】
【答案】
$864{\mathrm{cm} ^3}$
【解析】
如图,所折叠成的多面体是由一个大正三棱锥切去三个小正三棱锥得到的,所求体积为$$V = \dfrac{1}{3} \times \dfrac{1}{2} \times {18^3} - 3 \times \dfrac{1}{3} \times \dfrac{1}{2} \times {6^3} = 864{\mathrm{cm} ^3}.$$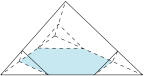

题目
答案
解析
备注