已知正四棱柱 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$A{A_1} = 2AB$，则 $CD$ 与平面 $BD{C_1}$ 所成角的正弦值等于 \((\qquad)\)
【难度】
【出处】
2013年高考大纲卷（理）
【标注】
【答案】
A
【解析】
建立空间直角坐标系，求出直线的方向向量与平面的法向量的夹角余弦值的绝对值，即为所求正弦值．以D为原点，$DA、DC、DD_1$ 所在的直线分别为 $x$ 轴、$y$ 轴、$z$ 轴建立空间直角坐标系，如图所示．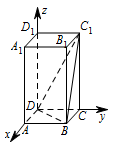
设 $AB=a$，则 $D\left(0,0,0\right)$，$B\left(a,a,0\right)$，$C_1\left(0,a,2a\right)$，$C\left(0,a,0\right)$．
设平面 $BDC_1$ 的一个法向量为 $\overrightarrow n=\left(x,y,z\right)$，则\[ \begin{cases}\overrightarrow n\cdot \overrightarrow {DB}=0,\\\overrightarrow n\cdot \overrightarrow {DC_1}=0.\end{cases} \]即\[ \begin{cases}ax+ay=0,\\ay+2az=0.\end{cases} \]令 $z=1$，可得\[\overrightarrow n=\left(2,-2,1\right).\]又\[\overrightarrow {CD}=\left(0,-a,0\right),\]所以 $CD$ 与平面 $BD{C_1}$ 所成角 $\theta$ 的正弦值为\[\sin \theta=|\cos<\overrightarrow n,\overrightarrow {CD}>|=\dfrac 23.\]即为所求．
设 $AB=a$，则 $D\left(0,0,0\right)$，$B\left(a,a,0\right)$，$C_1\left(0,a,2a\right)$，$C\left(0,a,0\right)$．设平面 $BDC_1$ 的一个法向量为 $\overrightarrow n=\left(x,y,z\right)$，则\[ \begin{cases}\overrightarrow n\cdot \overrightarrow {DB}=0,\\\overrightarrow n\cdot \overrightarrow {DC_1}=0.\end{cases} \]即\[ \begin{cases}ax+ay=0,\\ay+2az=0.\end{cases} \]令 $z=1$，可得\[\overrightarrow n=\left(2,-2,1\right).\]又\[\overrightarrow {CD}=\left(0,-a,0\right),\]所以 $CD$ 与平面 $BD{C_1}$ 所成角 $\theta$ 的正弦值为\[\sin \theta=|\cos<\overrightarrow n,\overrightarrow {CD}>|=\dfrac 23.\]即为所求．
题目
答案
解析
备注
