查看数据源：599165c12bfec200011e028a
已知抛物线 $C:{y^2} = 8x$ 与点 $M\left( { - 2,2} \right)$，过 $C$ 的焦点且斜率为 $k$ 的直线与 $C$ 交于 $A,B$ 两点，若 $\overrightarrow {MA} \cdot \overrightarrow {MB} = 0$，则 $k = $  \((\qquad)\)
A: $\dfrac{1}{2}$
B: $\dfrac{\sqrt 2 }{2}$
C: $\sqrt 2 $
D: $2$
【难度】
【出处】
2013年高考大纲卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    抛物线
    >
    抛物线的几何量
    >
    抛物线的基本量与几何性质
  • 知识点
    >
    向量
    >
    向量的运算
    >
    向量的数量积
  • 知识点
    >
    解析几何
    >
    直线与圆锥曲线
    >
    联立及韦达定理
【答案】
D
【解析】
本题中直线过焦点，可以考虑将题中问题向抛物线定义转化，结合 $\overrightarrow {MA} \cdot \overrightarrow {MB} = 0$，得知 $M$ 与 $AB$ 中点的连线平行于 $x$ 轴．由抛物线 $ C $ 的准线方程为 $ x=-2 $ 可知，点 $ M $ 在准线上，设直线方程为\[ y=k\left(x-2\right) ,\]并设 $ A\left(x_1,y_1\right) $，$ B\left(x_2,y_2\right) $，由 $\overrightarrow {MA} \cdot \overrightarrow {MB} = 0$ 可得 $ AM\perp BM $，所以点 $ M $ 到直线 $ AB $ 中点 $N$ 的距离等于 $ AB $ 弦长的一半，根据抛物线的定义，也即 $ AB $ 的中点 $ N $ 到准线的距离，所以线段 $ MN $ 即为三角形 $ MBA $ 的中线，所以 $ MN $ 平行于 $ x $ 轴，如图所示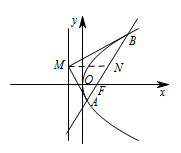： 则 $ N $ 点的纵坐标为 $ 2 $，而 $ y_1+y_2=4 $，联立直线方程与抛物线方程得\[ \dfrac k8y^2-y-2k=0, \]于是\[y_1+y_2=\dfrac 8k=4 ,\]解得 $ k=2 $．
题目 答案 解析 备注
0.115069s