如图，矩形纸片 $ABCD$ 中，$AB=4$，$BC=8$，将纸片沿 $EF$ 折叠，使点 $C$ 与点 $A$ 重合，则下列说法中：
① $AF=AE$
② $\triangle ABE\cong \triangle AGF$
③ $EF=2\sqrt 5$
④ $AF=EF$
结论正确的是 ．
① $AF=AE$
② $\triangle ABE\cong \triangle AGF$
③ $EF=2\sqrt 5$
④ $AF=EF$
结论正确的是
【难度】
【出处】
无
【标注】
【答案】
①②③
【解析】
由折叠性质得：$\angle AEF=\angle CEF$，$AE=CE$，$AG=CD$．
因为 $ AD\parallel BC$，
所以 $\angle AFE=\angle FEC$，
所以 $ \angle AEF=\angle AFE$，
所以 $ AF=AE$．
所以 $ \triangle ABE\cong \triangle AGF$．（$\mathrm{HL}$）
由勾股定理得：$AB^2+BE^2=AE^2$，
解得 $BE=3$，$AE=5$．
过点 $E$ 作 $AD$ 的垂线，垂足为 $M$．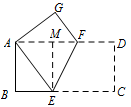
由勾股定理得：$EF^2=EM^2+FM^2$，
解得 $EF=2\sqrt 5$．
因为 $\angle FAE\neq 60^\circ$，
所以 $AF\neq EF$．
因为 $ AD\parallel BC$，
所以 $\angle AFE=\angle FEC$，
所以 $ \angle AEF=\angle AFE$，
所以 $ AF=AE$．
所以 $ \triangle ABE\cong \triangle AGF$．（$\mathrm{HL}$）
由勾股定理得：$AB^2+BE^2=AE^2$，
解得 $BE=3$，$AE=5$．
过点 $E$ 作 $AD$ 的垂线，垂足为 $M$．
由勾股定理得：$EF^2=EM^2+FM^2$，解得 $EF=2\sqrt 5$．
因为 $\angle FAE\neq 60^\circ$，
所以 $AF\neq EF$．
题目
答案
解析
备注
