如图，用 $35$ 个单位正方形拼成一个矩形，点 $P_1,P_2,P_3,P_4$ 以及四个标记为 $\blacktriangle$ 的点在正方形的顶点处．设集合 $\Omega=\left\{P_1,P_2,P_3,P_4\right\}$，点 $P\in\Omega$．过 $P$ 作直线 $l_P$，使得不在 $l_P$ 上的 $\blacktriangle$ 的点分布在 $l_P$ 的两侧．用 $D_1(l_P)$ 和 $D_2(l_P)$ 分别表示 $l_P$ 一侧和另一侧的 $\blacktriangle$ 的点到 $l_P$ 的距离之和．若过 $P$ 的直线 $l_P$ 中有且仅有一条满足 $D_1(l_P)=D_2(l_P)$，则 $\Omega$ 中所有这样的 $P$ 为 ．
【难度】
【出处】
无
【标注】
【答案】
$P_1,P_3,P_4$
【解析】
如图建系，设 $4$ 个 $\blacktriangle$ 的坐标分别为 $(0,3),(1,0),(4,4),(7,1)$，且 $P_1(0,4)$，$P_2(3,2)$，$P_3(4,2)$，$P_4(6,5)$．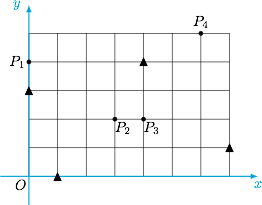
设直线 $l:Ax+By+C=0$，则条件 $D_1(l)=D_2(l)$ 即\[\sum_{i=1}^{4}\dfrac{A\cdot x_i+B\cdot y_i+C}{\sqrt{A^2+B^2}}=0,\]其中 $(x_i,y_i)$（$i=1,2,3,4$）表示 $4$ 个 $\blacktriangle$ 的坐标．也即\[\sum_{i=1}^4x_iA+\sum_{i=1}^4y_iB+4C=0,\]化简得\[3A+2B+C=0.\]因此题中条件等价于 $l_P$ 过点 $(3,2)$，该点即 $P_2$．因此 $P_1,P_3,P_4$ 符合题意．
设直线 $l:Ax+By+C=0$，则条件 $D_1(l)=D_2(l)$ 即\[\sum_{i=1}^{4}\dfrac{A\cdot x_i+B\cdot y_i+C}{\sqrt{A^2+B^2}}=0,\]其中 $(x_i,y_i)$（$i=1,2,3,4$）表示 $4$ 个 $\blacktriangle$ 的坐标．也即\[\sum_{i=1}^4x_iA+\sum_{i=1}^4y_iB+4C=0,\]化简得\[3A+2B+C=0.\]因此题中条件等价于 $l_P$ 过点 $(3,2)$，该点即 $P_2$．因此 $P_1,P_3,P_4$ 符合题意．
题目
答案
解析
备注
