已知直线 $l_1$ 的方程为:$ax+y-a-2=0(a>0)$,分别交 $x$ 轴,$y$ 轴于 $A, B$ 两点.
【难度】
【出处】
无
【标注】
-
(Ⅰ)求原点到直线 $l_1$ 距离的最大值及此时直线 $l_1$ 的方程;标注答案直线 $l_1$ 的方程为 $x+2y-5=0$解析略
-
(Ⅱ)若 $a$ 为常数,直线 $l_2:mx+ny=1(m, n\in \mathbb{R})$ 与线段 $AB$ 有一个公共点,求 $ \sqrt{m^2+n^2}$ 的最小值 $f(a)$.标注答案
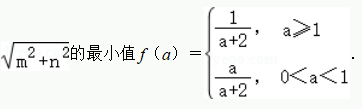 解析略
解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2