查看数据源：599165c12bfec200011e00f6
已知直三棱柱 $ABC - {A_1}{B_1}{C_1}$ 的 $ 6 $ 个顶点都在球 $ O$ 的球面上．若 $AB = 3$，$AC=4$，$AB\perp AC$，$A{A_1}=12$，则球 $ O$ 的半径为 \((\qquad)\)
A: $\dfrac {3 \sqrt {17}}{2} $
B: $2 \sqrt{10} $
C: $ \dfrac {13} 2 $
D: $3 \sqrt {10} $
【难度】
【出处】
2013年高考辽宁卷（文）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间组合体
    >
    空间几何体的接切
【答案】
C
【解析】
注意到该直三棱柱的底面为直角三角形，其 $6$ 个顶点均在一个球面上，可得到该三棱柱对应的长方体为该球的内接长方体，长方体的体对角线就是球的直径．过 $ C,B $ 分别作 $ AB,AC $ 的平行线，两线交于点 $ D $，过 $ C_1,B_1 $ 分别作 $ A_1B_1,A_1C_1 $ 的平行线，两线交于点 $ D_1 $，连接 $ DD_1 $，则 $ ABDC－A_1B_1D_1 C_1$ 恰为该球的内接长方体．长方体的三条边长分别为 $3,4,12$，所以对角线的长为\[\sqrt{3^2+4^2+12^2}=13,\]所以外接球$O$ 的半径为\[R=\dfrac{13}2.\]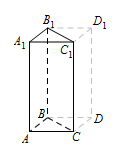 
题目 答案 解析 备注
0.114687s