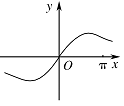
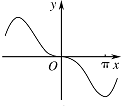
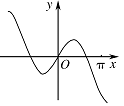
函数 $y = x\cos x + \sin x$ 的图象大致为 \((\qquad)\)
【难度】
【出处】
2013年高考山东卷(文)
【标注】
【答案】
D
【解析】
由解析式选图象的这类题,可以通过特殊值,奇偶性、单调性等函数的性质多方面考查,进而用排除法把不符合题意的排除.由函数奇偶性的运算性质可知,$y=x\cos x+\sin x$ 为奇函数,所以B选项错误;在 $x\in \left(0,\dfrac{\mathrm \pi} {2}\right)$ 上,$x>0$,$\cos x>0$,$\sin x>0$,所以 $y=x\cos x+\sin x>0\left(x\in \left(0,\dfrac{\mathrm \pi} {2}\right)\right)$,所以C选项错误;又 $f\left({\mathrm \pi} \right)=-{\mathrm \pi} <0$,故A选项错误,因此选D.
题目
答案
解析
备注