如图，将一张边长为 $1$ 的正方形纸 $ABCD$ 折叠，使得点 $B$ 始终落在边 $AD$ 上．
$(1)$ 折起部分面积的最小值为 ；
$(2)$ 线段 $EF$ 划过的面积为 ．
$(1)$ 折起部分面积的最小值为
$(2)$ 线段 $EF$ 划过的面积为
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 38$；$\dfrac{7}{24}$
【解析】
如图，作 $B'K\perp BC$ 于 $K$，连接 $BK$，则不难得到 $EF$ 始终与以 $B$ 为焦点，直线 $AD$ 为准线的抛物线相切于点 $K$．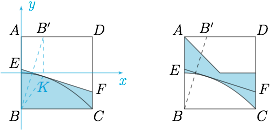
$(1)$ 以 $AB$ 的中点为原点建立平面直角坐标系，则图中的抛物线方程为 $x^2=-2y$．设 $K\left(2t,-2t^2\right)$，其中 $0\leqslant t\leqslant \dfrac 12$，则直线 $EF$ 的方程为$$2tx=-\left(y-2t^2\right),$$即$$y=-2tx+2t^2,$$因此折起部分的面积为\[\dfrac{2t^2+\dfrac 12+\left(-2t+2t^2\right)+\dfrac 12}{2}\cdot 1=2t^2-t+\dfrac 12\geqslant \dfrac 38,\]等号当 $t=\dfrac 14$ 时取得．因此所求的最小值为 $\dfrac 38$．
$(2)$ 由 $(1)$，可以求得所求面积为\[1-\dfrac 38-\int_0^1{\left(\dfrac 12-\dfrac 12x^2\right)}{\mathrm d}x=\dfrac{7}{24}.\]
$(1)$ 以 $AB$ 的中点为原点建立平面直角坐标系，则图中的抛物线方程为 $x^2=-2y$．设 $K\left(2t,-2t^2\right)$，其中 $0\leqslant t\leqslant \dfrac 12$，则直线 $EF$ 的方程为$$2tx=-\left(y-2t^2\right),$$即$$y=-2tx+2t^2,$$因此折起部分的面积为\[\dfrac{2t^2+\dfrac 12+\left(-2t+2t^2\right)+\dfrac 12}{2}\cdot 1=2t^2-t+\dfrac 12\geqslant \dfrac 38,\]等号当 $t=\dfrac 14$ 时取得．因此所求的最小值为 $\dfrac 38$．$(2)$ 由 $(1)$，可以求得所求面积为\[1-\dfrac 38-\int_0^1{\left(\dfrac 12-\dfrac 12x^2\right)}{\mathrm d}x=\dfrac{7}{24}.\]
题目
答案
解析
备注
