设整数 $n \geqslant 4$,集合 $X = \left\{ {1,2,3, \cdots ,n} \right\}$.令集合 $S = \left\{ {\left( {x,y,z} \right)\left|\right.x,y,z \in X} \right.,且三条件x < y < z,y < z < x,z < x < y\left. {恰有一个成立} \right\}$,若 $\left( {x,y,z} \right)$ 和 $\left( {z,w,x} \right)$ 都在 $S$ 中,则下列选项正确的是 \((\qquad)\)
【难度】
【出处】
2013年高考广东卷(理)
【标注】
【答案】
B
【解析】
集合 $S$ 中的元素需要满足三个条件中一个,故可对元素 $(x,y,z)$,$(z,\omega ,x)$ 进行分情况讨论,及比较大小,然后再确定选项中的两个元素是否在集合 $S$ 中.因为 $\left( {x,y,z} \right)\in S$,所以 $ x $,$ y $,$ z $ 的大小关系有 $ 3 $ 种;同理 $ z$,$w$,$x$ 的大小关系也有 $ 3 $ 种.如图所示,可知 $ x $,$ y $,$ w $,$ z $ 的大小关系有 $ 4$ 种,均符合 $\left( {y,z,w} \right) \in S$,$\left( {x,y,w} \right) \in S$.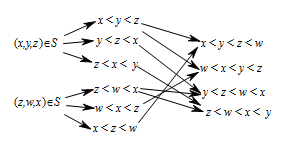

题目
答案
解析
备注