查看数据源：597ea5acd05b900009165206
已知函数 $f\left( x \right)$ 是定义在 ${\mathbb{R}}$ 上的奇函数，当 $x \geqslant 0$ 时，$$f\left( x \right) = \dfrac{1}{2}\left({\left|{x-{a^2}}\right| + \left|{x-2{a^2}}\right|-3{a^2}}\right).$$若 $\forall x \in{\mathbb{R}}$，$f\left({x-1}\right) \leqslant f\left( x \right)$，则实数 $a$ 的取值范围为 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    绝对值函数
  • 题型
    >
    不等式
    >
    恒成立与存在性问题
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的图象变换
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的奇偶性
【答案】
$\left[{-\dfrac{\sqrt 6}{6},\dfrac{\sqrt 6}{6}}\right]$
【解析】
当 $a\neq 0$ 时，用分界点 $x=a^2$ 和 $x=2a^2$ 讨论，结合函数的奇偶性，不难画出函数的草图如图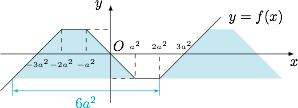．题中条件“$\forall x\in{\bf R},f(x-1)\leqslant f(x)$”的含义是将函数图象向右平移 $1$ 个单位，设法将图象中的“山”（阴影部分）移动到原图象的下方（可以与边界重合）．因此有 $6a^2\leqslant 1$．结合 $a=0$ 时显然符合题意，可解得实数 $a$ 的取值范围是 $\left[{-\dfrac{\sqrt 6}{6},\dfrac{\sqrt 6}{6}}\right]$．
题目 答案 解析 备注
0.111806s