如图,过圆 $C:(x-1)^2+(y-1)^2=1$ 的圆心,作直线分别交 $x,y$ 正半轴于点 $A,B$,$\triangle{AOB}$ 被圆分成四部分,若这四部分图形面积满足 $S_{\rm{I}}+S_{\text{Ⅳ}}=S_{\text{Ⅱ}}+S_{\rm{III}}$,则这样的直线 $AB$ 有 条.

【难度】
【出处】
无
【标注】
【答案】
$1$
【解析】
容易发现 $S_{\rm{II}}$ 和 $S_{\rm{IV}}$ 是定值,所以 $S_{\rm{III}}-S_{\rm{I}}=S_{\rm {IV}}-S_{\rm {II}}$.如图,作直线关于 $y=x$ 对称的直线,从而作出 $S_{\rm{III}}-S_{\rm{I}}$.容易发现随着直线 $AB$ 斜率的减小,$S_{\rm{III}}-S_{\rm{I}}$ 递增.因此,这样的直线 $AB$ 只有 $1$ 条.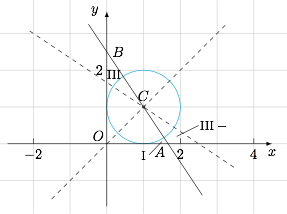

题目
答案
解析
备注